24.小云在学习过程中遇到一个函数y=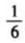|x(x²-x+1)(x≥-2).

下面是小云对其探究的过程,请补充完整:

(1)当-2≤x<0时,

对于函数y1=|x|,即y1=-x,当-2≤x<0时,y随x的增大而________且y₁>0;

对于函数y₂=x²-x+1,当-2≤x<0时,y₂随x的增大而_________且y₂>0;

结合上述分析,进步探究发现,对于函数y,当-2≤x<0时,y随x的增大而_______

(2)当x≥0时,

对于函数y,当x≥0时,y与x的几组对应值如下表:

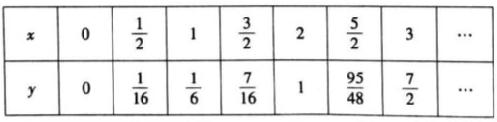
结合上表,进一步探究发现,当x≥0时,y随x的增大而增大,在平面直角坐标系xOy中,画出当x≥0时的函数y的图象

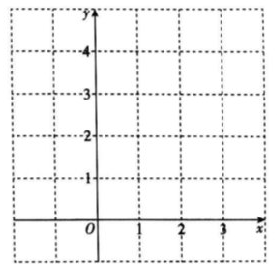
(3)过点(0,m)(m>0)作平行于x轴的直线l,结合(1)(2)的分析,解决问题:若直线l与函数y=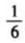|x|(x²-x+1)(x≥-2)的图象有两个交点,则m的最大值是______________。

19.已知5x²-x-1=0,求代数式(3x+2)(3x-2)+x(x-2)的值.

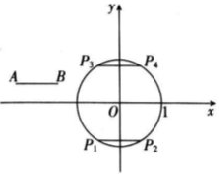
28.在平面直角坐标系xy中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦AB(A,B分别为点A,B的对应点),线段AA长度的最小值称为线段AB到⊙O的“平移距离”

(1)如图,平移线段AB得到⊙O的长度为1的弦P₁P₂和P₃P₄,则这两条弦的位置关系是__________;在点P₁,P₂,P₃,P₄中,连接点A与点______的线段的长度等于线段AB到⊙O的“平移距离”;

(2)若点A,B都在直线y=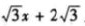上,记线段AB到⊙O的“平移距离”为d₁,求d₁的最小值;

(3)若点A的坐标为(2,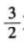),记线段AB到⊙O的“平移距离”为d₂,直接写出d₂的取值范围;

22.在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象由函数y=x的图象平移得到,且经过点(1,2).

(1)求这个一次函数的解析式;

(2)当x>1时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b的值,直接写出m的取值范围

8.有一个装有水的容器,如图所示,容器内的水面高度是10cm,现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒0.2cm的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是

25.小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:

a.小云所住小区5月1日至30日的厨余垃圾分出量统计图:

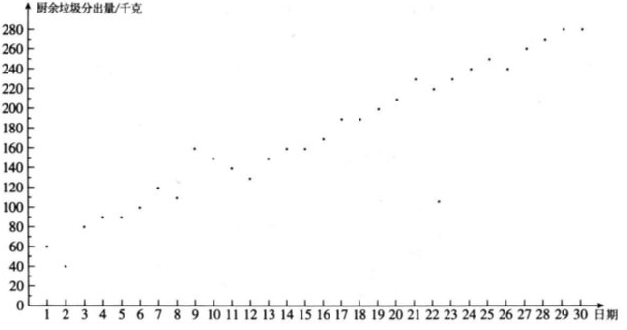
b.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:

(1)该小区5月1日至30日的厨余垃圾分出量的平均数约为___________(结果取整数);

(2)已知该小区4月的厨余垃圾分出量的平均数为60,则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的________倍(结果保留小数点后一位);

(3)记该小区5月1日至10日的厨余垃圾分出量的方差为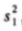,5月11日至20日的厨余垃圾分出量的方差为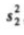,5月21日至30日的厨余垃圾分出量的方差为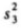.直接写出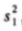,,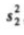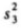的大小关系

26.在平面直角坐标系xy中,M(x₁,y₁),N(x₂,y₂)为抛物线y=ax²+bx+c(a>0)上任意两点,其中x1<x2

(1)若抛物线的对称轴为x=1,当x₁,x₂为何值时,y₁=y₂=c;

(2)设抛物线的对称轴为x=t.若对于x₁+x₂>3,都有y₁<y₂,求t的取值范围

7.不透明的袋子中有两个小球,上面分别写着数字“1”,“2”,除数字外两个小球无其他差别从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为3的概率是

17.计算:

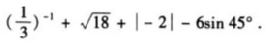
10.已知关于x的方程x²+2x+k=0有两个相等的实数根,则k的值是__________